Affirming a disjunct
The logical fallacy of affirming a disjunct also known as the fallacy of the alternative disjunct or a false exclusionary disjunct occurs when a deductive argument takes the following logical form:
- A or B
- A
- Therefore, it is not the case that B
Or in logical operators:
¬ 
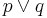
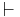Where 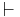denotes a logical assertion.
Contents |
Explanation
The fallacy lies in concluding that one disjunct must be false because the other disjunct is true; in fact they may both be true. This results from "or" being defined inclusively rather than exclusively. Affirming the disjunct should not be confused with the valid form known as the disjunctive syllogism.
Example
The following argument indicates the invalidity of affirming a disjunct:
- Max is a cat or Max is a mammal.
- Max is a cat.
- Therefore, Max is not a mammal.
This inference is invalid. If Max is a cat then Max is also a mammal. (Remember "or" is defined in an inclusive sense not an exclusive sense.)
- The car is red or the car is large.
- The car is red.
- Therefore, the car is not large.
The above example of an argument also demonstrates the fallacy.
See also
External links
|
|||||||||||||||||